
Zadanie Biuro podróży (biu)
Pomóż nam usprawnić bazę zadań!
Biuro podróży
Limit pamięci: 32 MB
W ostatnim czasie mieszkańcy Bajtocji zaczęli podróżować częściej niż
dotychczas. Przedsiębiorczy Bajtazar wpadł na pomysł otwarcia biura
podróży. Już pierwszego dnia urzędowania do biura zgłosiło się  klientów
(na potrzeby naszego zadania możemy ich ponumerować liczbami
naturalnymi od
klientów
(na potrzeby naszego zadania możemy ich ponumerować liczbami
naturalnymi od 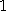 do
do  ), którzy chcą pojechać na wycieczkę.
Niestety każdy z nich ma swoje wymagania.
), którzy chcą pojechać na wycieczkę.
Niestety każdy z nich ma swoje wymagania.
Twoim zadaniem jest pomóc Bajtazarowi w wybraniu klientów, którzy pojadą na wycieczkę, tak aby zmaksymalizować zysk Bajtazara.
Każdy klient określił, ile wynosi dla niego wartość wycieczki organizowanej przez
Bajtazara. Niech 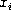 będzie taką wartością dla klienta
będzie taką wartością dla klienta 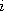 (
(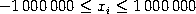 ).
Jeśli
).
Jeśli 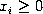 , to klient
, to klient 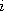 zapłaci
zapłaci 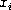 bajtockich dolarów,
aby pojechać na wycieczkę, jeśli natomiast
bajtockich dolarów,
aby pojechać na wycieczkę, jeśli natomiast 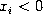 ,
to aby klient
,
to aby klient  pojechał na wycieczkę, Bajtazar musi mu
dopłacić
pojechał na wycieczkę, Bajtazar musi mu
dopłacić 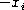 bajtockich dolarów.
bajtockich dolarów.
Klienci oprócz wymagań finansowych posiadają również wymagania towarzyskie.
Klient 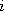 ma
ma  (
(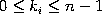 ) takich wymagań,
) takich wymagań,
 -te wymaganie
-te wymaganie 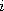 -tego klienta jest reprezentowane przez parę
liczb całkowitych (
-tego klienta jest reprezentowane przez parę
liczb całkowitych ( )
(
)
(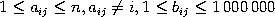 ).
Wymaganie to należy rozumieć tak, że aby klient
).
Wymaganie to należy rozumieć tak, że aby klient 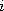 pojechał na wycieczkę, to na wycieczkę musi pojechać również klient
pojechał na wycieczkę, to na wycieczkę musi pojechać również klient
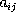 lub koszt wycieczki dla klienta
lub koszt wycieczki dla klienta 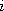 musi zostać obniżony o
musi zostać obniżony o 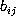 bajtockich dolarów (może się zdarzyć, że koszt wycieczki dla pewnych klientów
z dodatniego stanie się ujemny, co spowoduje, że Bajtazar będzie musiał dopłacić tym
klientom, żeby wzięli oni udział w wycieczce, rekompensując tym samym brak zaspokojenia
ich wymagań towarzyskich).
bajtockich dolarów (może się zdarzyć, że koszt wycieczki dla pewnych klientów
z dodatniego stanie się ujemny, co spowoduje, że Bajtazar będzie musiał dopłacić tym
klientom, żeby wzięli oni udział w wycieczce, rekompensując tym samym brak zaspokojenia
ich wymagań towarzyskich).
Pomóż Bajtazarowi wybrać grupę klientów, których ma zabrać na wycieczkę, tak aby zmaksymalizować jego zysk (liczba miejsc na wycieczce jest nieograniczona).
Zadanie
Dysponujesz jedenastoma zestawami danych, które możesz ściągnąć stąd.
Każdy zestaw jest zapisany w osobnym pliku biu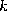 .in, gdzie
.in, gdzie
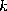 to numer zestawu (
to numer zestawu (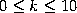 ). Rozwiązaniem zadania powinien być
program, który wczytuje ze standardowego wejścia jedną liczbę
całkowitą
). Rozwiązaniem zadania powinien być
program, który wczytuje ze standardowego wejścia jedną liczbę
całkowitą 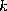 , i wypisuje na standardowe wyjście
odpowiedź dla
, i wypisuje na standardowe wyjście
odpowiedź dla 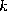 -tego zestawu.
Rozwiązanie zestawu biu0.in nie jest
punktowane.
-tego zestawu.
Rozwiązanie zestawu biu0.in nie jest
punktowane.
W pierwszym wierszu odpowiedzi powinna się znajdować dokładnie jedna liczba całkowita 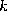 (
( )
- liczba klientów, których Bajtazar powinien zabrać na wycieczkę.
Jeśli liczba
)
- liczba klientów, których Bajtazar powinien zabrać na wycieczkę.
Jeśli liczba 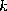 jest dodatnia, w drugim wierszu powinno się znaleźć
jest dodatnia, w drugim wierszu powinno się znaleźć 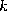 liczb całkowitych, oddzielonych pojedynczymi odstępami,
będących numerami klientów, których Bajtazar powinien zabrać na wycieczkę.
Jeśli istnieje wiele optymalnych rozwiązań to możesz podać dowolne z nich.
Numery klientów mogą być umieszczone w wyjściu w dowolnej kolejności.
liczb całkowitych, oddzielonych pojedynczymi odstępami,
będących numerami klientów, których Bajtazar powinien zabrać na wycieczkę.
Jeśli istnieje wiele optymalnych rozwiązań to możesz podać dowolne z nich.
Numery klientów mogą być umieszczone w wyjściu w dowolnej kolejności.
Opis pojedynczego pliku wejściowego
W pierwszym wierszu znajduje się dokładnie jedna liczba całkowita  (
(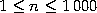 )
oznaczająca liczbę klientów biura podróży.
W kolejnych
)
oznaczająca liczbę klientów biura podróży.
W kolejnych  wierszach opisani są poszczególni klienci.
W
wierszach opisani są poszczególni klienci.
W 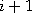 -wszym wierszu (
-wszym wierszu ( ) znajdują się liczby całkowite
) znajdują się liczby całkowite 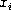 (
(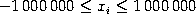 ) oraz
) oraz 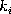 (
(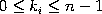 ),
a za nimi
),
a za nimi 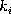 par liczb całkowitych
par liczb całkowitych 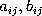 ,
(
,
(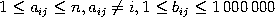 )
- wszystkie liczby w wierszu
oddzielone są pojedynczymi odstępami. Możesz założyć, że każdy klient ma co najwyżej
jedno wymaganie towarzyskie dotyczące dowolnego innego klienta.
)
- wszystkie liczby w wierszu
oddzielone są pojedynczymi odstępami. Możesz założyć, że każdy klient ma co najwyżej
jedno wymaganie towarzyskie dotyczące dowolnego innego klienta.
Przykład
Dla danych wejściowych:4 5 0 6 2 1 10 3 1 -10 0 1 2 1 10 2 10poprawną odpowiedzią jest:
3 1 2 4
Jeśli Bajtazar wybierze klientów 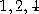 , to osiągnie zysk
, to osiągnie zysk 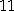 bajtockich dolarów,
co jest rozwiązaniem optymalnym.
bajtockich dolarów,
co jest rozwiązaniem optymalnym.
Autor zadania: Marek Cygan.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English